Playing Games with Infinity
What do Borges, DFW + consciousness have in common
[ There is a concept which corrupts and upsets all others, Jorge Luis Borges ]
Infinity is the concept referred to by Borges above, taken from his essay Avatars and the Tortoise. The quote acted as the original epitaph for David Wallace’s Good Old Neon, a story which is doubly haunted by infinity itself, and the ghosts of its avatars. In Neon, Wallace incorporates different construals of infinity by referencing problems they pose in mathematical logic, and then reflecting these in the narrative structure itself. In doing so, he constructs a story that enacts what it explores; the way out of our own heads, an escape from the “infinities” of a conscious self and its infinite regress. Not through sublimating complexity, but accepting finitude so it cannot torment us. Not through conquering infinity, but playing games with it so it does not overwhelm us.
i. Strange loops
It is not the idea of infinity itself that occasions intellectual horror, but its avatars; those other concepts it corrupts. It is they who horrify and torment, to the extent that they reveal and impose limitations, denying us comprehension or easy containment. In Avatars, Borges outlines Zeno’s second paradox motion, ‘Achilles and the Tortoise’, which upsets our conception of space[1]. The reasoning behind the paradox asserts the impossibility of movement on the basis that any moving object will need to cover half the distance to its destination, before which it will need to cover half of that, and half of that, and so on ad infinitum. In Good Old Neon, the same “vertiginous regressus in infinitum[2]” that is “perhaps applicable to all subjects[3]” becomes manifest in consciousness itself.
Infinity paradoxes[4], such as the “Russell” and “Berry” paradoxes mentioned in the text by Wallace, are those that arise from self reference, a turning in on themselves. The former relates to naïve set theory, with the problematic construction of the set of all sets that are not members of themselves. Berry’s paradox relates to the description of unique numbers, and is a semantic, rather than logical, paradox of self-reference:
“that the very smallest number that can’t be described in under twenty-two syllables … is itself a description of this number, only has twenty-one syllables in it”.
Analogies have been drawn between such looping self-referentiality and conceptions of consciousness as a strange loop[5], as opposed to any stable or singular self. The association between consciousness, self-reference and infinite regress is prefigured more indirectly by the story’s opening line, which transfers the infinity paradoxes that reside in language or logic to consciousness itself. Neal’s declaration “I am a fraud” articulates a version of the Liar’s Paradox, which, like Berry’s, is a semantic one. Its most basic formulation is the following: “this statement is false”. The “this” points to the statement itself in the same way that Neal’s “I am a fraud” points to the ‘self’ that is speaking. A contradiction results, oscillating between truth and falsity, dissolving the “fraudulence paradox” into a “vicious infinite regress”, the same wording Wallace uses to describe Zeno’s paradox in his treatise on infinity[6].
That the statement cannot possess a consistent truth value is a direct result of self-referentiality. The opening admission is confessed not just to us, the “you” that is the reader, but also to Dr Gustaffson, giving rise to his conclusion that Neal could not possibly be a fraud if he “was capable of admitting it”. Yet this apparent “reductio ad absurdum” fails to provide any resolution, fails to actually solve the paradox, as Neal tells us “the real truth”, that his “confession of being a fraud and of having wasted time sparring with him over the previous weeks in order to manipulate him into seeing me as exceptional and insightful had itself been kind of manipulative.” Here the hypotactic constructions and rhetorical mirroring of “manipulate” reflect this recursion, the vicious cycle of Neal’s own hyper-reflectivity and self-awareness. Even after this “real truth”, Neal expresses a fear he “is trapped in this false way of being and unable ever to… tell the truth”. The mental contortions, the constant qualifications and equivocations, depict a consciousness doubling back on and devouring itself. So it is not the quality (of fraudulence) that is itself problematic; Wallace queries, towards the end, whether you can actually “be a fraud if you are unaware you are a fraud?”. It is the awareness of it, the consciousness belonging to the “I” of the speaker, which both constructs this “trap” and precludes any possibility of escape from it.
ii. The cage of consciousness
Implicit in the accusation of being a “fraud” is the existence of some authentic or coherent self that remains just out of reach. The reason this ‘gap’ between the two exists, through which fraudulence can emerge, is yet “another paradox”:
“Many of the most important impressions and thoughts in a person’s life are ones that flash through your head so fast that fast isn’t even the right word they seem totally different from or outside of the regular sequential clock time we all live by, and they have so little relation to the sort of linear, one-word-after- another-word English we all communicate with each other with that it could easily take a whole lifetime just to spell out the contents of one split-second’s flash of thoughts and connections, etc.”.
Neal identifies the disjunct that arises between the inconceivable rapidity of conscious thought - the “universes inside you” - and the finitude of language which cannot contain it, even as he attempts such a task. If he is trapped in this cage of consciousness, then, it is by “words and chronological time”, which create all these “misunderstandings”, that he is chained. For Neal, the problem of conquering infinity, of achieving self-reference without paradox or consciousness without infinite regress, lies in overcoming these constraints. It is in another problem of mathematical logic, Gödel’s “incompleteness theorem”, that we find a possible solution. Gödel used self-referential, or meta-mathematical, statements to show that in any attempt to construct a formal system of arithmetic, there will be axioms – statements about properties within that system - which cannot be proven within it. Self-reference in this sense revealed necessary incompleteness - the system must step outside itself to account for itself. In Neal’s case, the recursive traps of thought might only be escaped by such a move: finding a vantage beyond the closed system of his own self-reflexivity.
iii. On human limits
Neal’s preoccupation with such a ‘stepping out’ as a way of mastering infinity emerges in his discussion of time. We are told that“impressions and thoughts” are “outside of the regular sequential clock time we all live by”. Theorems are true “everywhere and all the time” because “logic is totally abstract and outside what we think of as time”. The dream Neal has of the statute, a “warning” against fraudulence delivered by his subconscious, takes place in “dream time as opposed to waking, chronological time”. An implicit opposition is established between these things; those “abstract and universal” truths, which exist “outside time”, and the waking conscious self, the logical contradictions, that exist ‘in time’. Time, then, is associated with precluding both more stable knowledge and a stable ‘self’.
It is not until the first and only footnote that we are presented with a possible escape-route from the dizzying circularity of Neal’s rhetoric so far. The footnote enacts a stepping out of this system, existing ‘outside’ the temporal bounds of the main narrative and physically separated from it on the page. In it we find a refutation of that same system; what the footnote describes, the “various paradoxes” of time, it replicates on the level of narrative structure. The “*” exists in the narrowest possible space between words in a linguistic equivalent of Zeno’s paradox. It subdivides the instant that passes between them into ever more instants, contained in the footnote text itself, to disrupt any notion of succession or continuity through time. Just as Zeno signalled the impossibility of movement through space, the footnote asserts that “this now is infinite”, that “there is really no movement at all” in the temporal plane.
Borges presents a similar argument in his Refutation of Time. Yet he makes the observation that to embrace an infinite present – to “deny temporal succession[7]” - is to “deny the self”. That is how Neal and Dr. Gustafsson are able to have a “good laugh… after [they’d] both died and were outside linear time”. It is why being “outside time is not just an expression or manner of speaking”. To exist “outside time” is to die. It is in this narrative attempt to conquer infinity by escaping time, and destroying succession, that we reach Neal’s suicide.
The recursive loopiness of Neal’s own rhetoric is mirrored in the narrative structure itself, which circles around its conclusion. From the start, we are assured “it gets a lot more interesting when I get to the part where I kill myself”, and again halfway through “we’re getting to the part where I actually kill myself”, to the centre of this endless labyrinth. The narrative’s forward momentum has been carrying us towards it, the Minotaur that is Neal’s own “death in the fiery single-car accident”.
In the paragraph preceding the footnote we accelerate towards Neal’s death, “we’re coming to what [he] promised”, where the “Lily Cache slopes slightly down”. If time is “the car’s forward movement”, the footnote itself exists in and wholly constitutes that “literally immeasurable instant between impact and death”. Yet the repeated refrain of the main narrative “because listen – we don’t have much time… so listen” signals an urgency that contradicts the footnote’s contention that this “now” is “infinite”. It is because the “instant” must end, and it does, as we reach the centre of the labyrinth at the footnote’s conclusion: “THE END” signals Neal’s death just as language, this narrative thread, suffers the same fate. The text, that “instant”, can delay time but not transcend it; we are in language just as we exist in time. Time is, after all, the substance we are made of[8]. For Neal, the constraints imposed by temporality, and by extension, language, are insurmountable. Yet their destruction can free the self from its cage only by precipitating a complete annihilation of it.
The main narrative thread after the footnote continues with:
“The truth is you’ve already heard this. That this is what it’s like”,
an imperfect echo of the refrain appearing a page earlier:
“The truth is you already know what it’s like.”
The doubled refrain refuses closure, and it is with the second assertion of “this truth” that the narrative splinters. We have already trodden the path of mastery over infinity through death. It is here we come to the second, more provisional mode of living-with-and-through, of grappling with the “infinities you can never show another soul”. The alternative, to resolution by annihilation, is not to conquer paradox, but inhabit it fully. To persist is to play games with infinity.
iv. Games with infinity
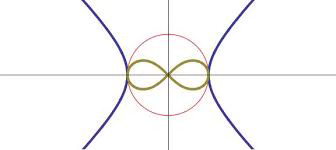
To contextualise these games it is necessary to first distinguish between different kinds of infinity. We have the inward-looking ‘bad’ infinities of paradox and reflectivity, characterised by circularity and recursive forms. We can conceive of ‘good’ infinities as those characterised by limits, convergence and asymptotes. These represent an endless outward expansion, a metastatic growth, rather than infinite regress. The difference can be seen visually in the shape of the lemniscate, a closed looping structure, compared to a hyperbola, which expands outwards (Fig. 1 below). The latter function is a mathematical inversion of the former, and so it is through inversion we can pass from one kind of infinity to the other.
An instance of such inversion plays out on the last page, when it is revealed that the narrative so far has not been narrated by Neal at all, but is actually:
“David Wallace… trying, through the tiny little keyhole of himself, to imagine what all must have happened to lead up to my death in the fiery single-car accident he’d read about in 1991”
With this revelation we jump out of the hypodiegetic level of Neal’s first-person perspective to the diegetic level of “Wallace’s” consciousness. This movement is less a stepping out than a turning outwards. Instead of exiting the system, it performs the function of Godel’s meta-mathematical constructions themselves – providing a new vantage point from which to view the system while remaining within it. This suggests that what the problem “really is, it turns out is a matter of perspective”. It is through this inversion of perspective, this metafictional twist, that we are able to transition between infinities. The rhetorical “I” is no longer Neal circling around himself, his suicide no longer the narratological centre of the labyrinth; both are limits towards which the series, being “Wallace”, converges.
It is through this inversion of the cage, this unravelling of consciousness, that we can escape it. “Wallace” is not, like Neal, chained by “words and chronological time”. Instead they are the escape-route, the exit, through which his consciousness branches out into the world. If death destroys time, and syntax is an essential time-bound dimension of language, then to write, to speak, to interpret, is to delay time, to postpone death.
In Refutations, Borges proposes the following: that if we can postulate in two individuals, on whom the same process is acting, two identical moments, then that one repeated term is enough to destroy time[13]. Death is such a moment that destroys time and succession; the only identical moment replicated in all minds.
Before the footnote, we find an extended metaphor of the self as an “enormous room”, of which “only parts” can “squeeze out… of tiny keyholes”. It is only “after what you think of as you has died” you can “open the door and be in anyone else’s room”. To enter the “room” would be to experience the exact same experience as the ‘sufferer’, in this case Neal. It would also create, in two people, this ‘identical moment’ identified above. If “Wallace” could step inside Neal’s mind at the time of his death, to completely understand the why behind it, he would have no choice but to die also. He too would meet the despair, the fiery death, at the labyrinth’s centre. But the footnote, in which Neal’s death takes place, is, in effect, outside the time of the story and so the main narrative thread, which is “Wallace’s” consciousness, cannot access it. It is only over time and through language that we can be known and know each other. We don’t have an “almost literal eternity”, and so all we can ever know is partial. We cannot “ever truly know what’s going on inside” another’s mind.
A sceptical reading would see “Wallace” left teetering on the brink of this abyss, the conclusion never reached - this unbridgeable gap between him and Neal. What this gap ensures, however, while it lasts, is that death remains just out of reach. The same features of language that Neal found insurmountable are the best safeguards against its extinction; the same Time that haunts Neal and, with the passing of that “immeasurable instant”, destroys him, saves “Wallace”. These essential constraints mean the process of knowing - of interpretation – is never complete, that the limit is never reached. They are the condition for constant motion, and it is this very deferral that sustains life against closure and stasis. That keeps us from collapsing into the “sort of inbent spiral that keeps you from ever getting anywhere”. True finitude would be the annihilation of conquered infinities, the claustrophobic closure of complete or instantaneous knowledge. Far better is it to play an infinite game, the possibilities of which can never be exhausted; to brush up, however briefly or incompletely, against the infinite corridors of another.
[1] Borges, J.L. (2011) ‘Avatars of the Tortoise’, in Labyrinths. Penguin.
[2] Ibid.
[3] Ibid.
[4] Gaifman, H. (1983). Paradoxes of infinity and self-applications, I. Erkenntnis, 20(2), 131–155. https://doi.org/10.1007/bf00153956.
[5] Hofstadter, D.R. (2008) I am a strange loop. New York: BasicBooks.
[6] Wallace, D.F. (2010) Everything and more: A compact history of infinity. New York: Atlas Books
[7] Borges, J.L. (2011) ‘A New Refutation of Time’, in Labyrinths. Penguin.
[8] Ibid.


I am glad you are back x